O que significa velocidade vetorial?
Sua noção de velocidade vetorial é provavelmente parecida com sua definição científica. Você sabe que um grande deslocamento em um curto espaço de tempo significa uma grande velocidade vetorial, e que velocidade tem unidades de distância dividida pelo tempo, como quilômetros por hora ou milhas por hora (unidade usada nos Estados Unidos).
Velocidade vetorial média é definida como a variação na posição divida pelo tempo de deslocamento.
Vmed = xΔ = xf − x0 Δt = tf − t0
vmed =Δt / Δx =xf−x0 /tf−t0
Nesta fórmula, é a velocidade vetorial média; Δx, é a mudança de posição, ou deslocamento; e x_fx fx, são as posições finais e iniciais nos tempos t_ftft, respectivamente. Se o tempo de início t_0t / 0t, é tomado como zero, então a velocidade vetorial média é escrita como abaixo:
Nota: ttt é uma abreviação de \Delta tΔtdelta, t. Observe que essa definição indica que a velocidade vetorial é um vetor porque o deslocamento é um vetor. A velocidade vetorial tem magnitude e direção. A unidade do SI para a velocidade vetorial é metros por segundo, mas muitas outras unidades como (também escrita como mph), e normalmente são usadas. Suponha, por exemplo, que um passageiro de um avião levou 5 segundos, −4 metros sendo que o sinal negativo indica que esse deslocamento foi na direção da parte de trás do avião. Sua velocidade vetorial média seria: vmed=tΔx=5 s−4 m=−0,8s mv, s
O sinal negativo indica que a velocidade vetorial média também é na direção da parte de trás do avião.Contudo, a velocidade vetorial média de um objeto não nos diz nada sobre o que acontece com ele entre o ponto inicial e o ponto final. Por exemplo, não podemos dizer, a partir da velocidade vetorial média, se o passageiro do avião para momentaneamente ou volta antes de ir para a parte de trás do avião.
Para obter mais detalhes, precisamos considerar pequenos segmentos do trajeto em intervalos de tempo pequenos. Por exemplo, na figura abaixo, vemos que o deslocamento total, consiste de 4 segmentos,
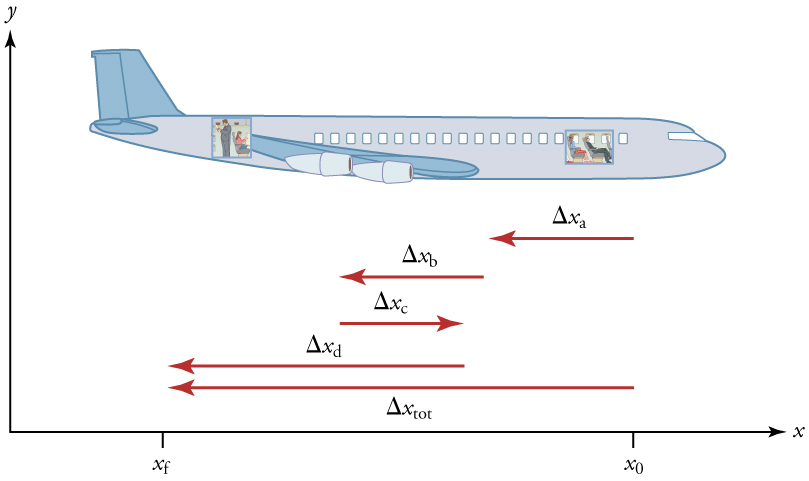
Figura 1: Um registro mais detalhado de um passageiro de avião indo em direção à parte traseira do avião, mostrando segmentos menores de seu trajeto. Figura: Openstax College Physics
Quanto menor o intervalo de tempo considerado em um movimento, mais detalhada é a informação. Levando esse processo para sua conclusão lógica, ficamos com um intervalo infinitamente pequeno. Em um intervalo assim, a velocidade vetorial média se torna a velocidade vetorial instantânea, ou a velocidade vetorial em um momento específico.
O velocímetro de um carro, por exemplo, mostra a magnitude (mas não a direção) da velocidade vetorial instantânea do carro. A polícia multa com base na velocidade vetorial instantânea, mas para calcular o tempo necessário para ir de um lugar a outro em uma viagem pela estrada, você precisa usar a velocidade vetorial média.
A velocidade vetorial instantânea vvv é simplesmente a velocidade vetorial média em um instante específico no tempo (ou em um intervalo de tempo infinitamente pequeno). Matematicamente, encontrar a velocidade vetorial instantânea, vvv, em um instante preciso ttt pode envolver encontrar um limite, uma operação de cálculo que está além do escopo deste artigo. Contudo, sob várias circunstâncias, podemos encontrar valores precisos para a velocidade vetorial instantânea sem usar cálculo.
O que significa velocidade escalar?
É importante entender que “velocidade escalar” e “velocidade vetorial” na física não têm o mesmo significado e são conceitos distintos. A maior diferença é que a velocidade escalar não tem direção. Ou seja, como o nome diz, é uma medida escalar.
Assim como precisamos distinguir entre velocidade vetorial instantânea e velocidade vetorial média, também precisamos distinguir entre velocidade escalar instantânea e velocidade escalar média.
Note que no dia a dia quando falamos apenas velocidade, estamos nos referindo à velocidade escalar, ou magnitude da velocidade vetorial.
Velocidade escalar instantânea é a magnitude da velocidade vetorial instantânea. Por exemplo, vamos supor que o passageiro do avião em um instante tinha uma velocidade vetorial instantânea de -3,0 o sinal negativo significa que ele se movia na direção da parte traseira do avião). Nesse mesmo tempo, sua velocidade escalar instantânea era de 3,0.
Ou suponha que em um dado instante durante uma viagem de compras sua velocidade vetorial instantânea é de 40 para o norte. Sua velocidade escalar instantânea naquele instante seria de 40 (isto é, a mesma magnitude mas sem uma direção). A velocidade escalar média, contudo, é muito diferente da velocidade vetorial média.
A velocidade escalar média é a distância percorrida dividida pelo tempo decorrido. Então, embora as magnitudes das velocidades escalar e vetorial instantâneas sejam sempre idênticas, as magnitudes das velocidades escalar e vetorial médias podem ser bem diferentes.
Como a distância percorrida pode ser maior que a magnitude do deslocamento, a velocidade escalar média pode ser maior que a magnitude da velocidade vetorial média. Por exemplo, se você dirige para uma loja e volta para casa em meia hora, e o hodômetro do seu carro mostra que a distância total percorrida foi de 6 km, então sua velocidade escalar média foi de 12 km/h. Sua velocidade vetorial média, contudo, foi zero, porque seu deslocamento na viagem de ida e volta é zero. (Deslocamento é a variação na posição e, portanto, é zero para uma viagem de ida e volta). Portanto, a velocidade escalar média não é simplesmente a magnitude da velocidade vetorial média.
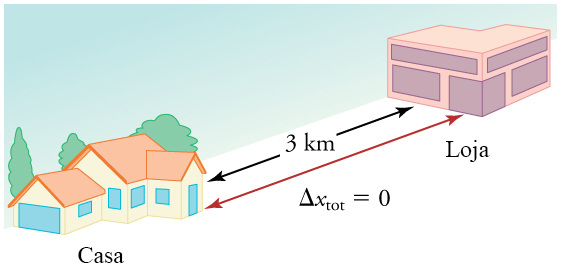
Figura 2: Durante uma viagem de ida e volta de 30 minutos até a loja, a distância total percorrida é de 6 km. A velocidade escalar média é de 12 km/h. O deslocamento na viagem de ida e volta é zero, já que não houve variação na posição. Portanto, a velocidade vetorial média é zero. (Figura: Openstax College Physics)Outra forma de visualizar o movimento de um objeto é usar um gráfico. Um gráfico da posição ou da velocidade vetorial como uma função do tempo pode ser muito útil. Por exemplo, para esse trajeto até a loja, os gráficos da posição, da velocidade vetorial e da velocidade escalar versus o tempo são exibidos na Figura 3. Observe que esses gráficos descrevem um modelo bastante simplificado do trajeto. Estamos considerando que a velocidade escalar é constante durante todo trajeto, o que não é realista, dado que provavelmente vamos parar na loja. Mas, para simplificar, não vamos considerar paradas ou alterações na velocidade escalar. Também estamos considerando que a rota entre a loja e a casa é uma linha perfeitamente reta.
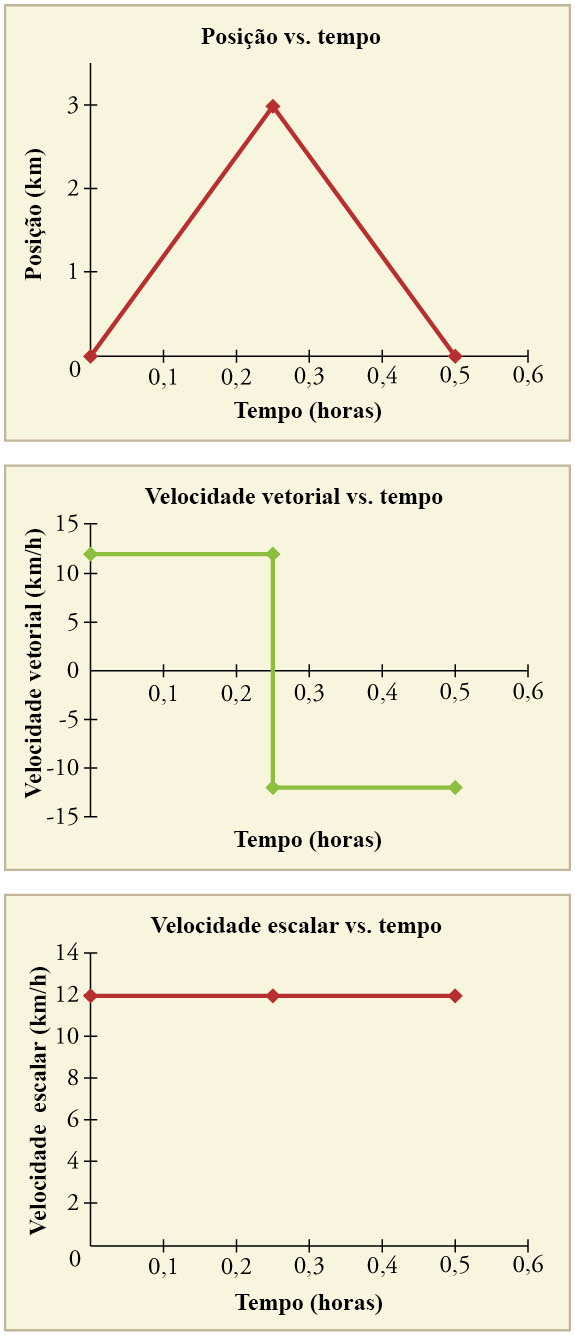
Figura 3: Posição vs. tempo, velocidade vetorial vs. tempo e velocidade escalar versus tempo em uma viagem. Observe que a velocidade vetorial para a viagem de volta é negativa. (Figura: Openstax College Physics)
Como são exemplos resolvidos envolvendo as velocidades vetorial e escalar?
Exemplo 1: A iguana desorientada
Uma iguana com um senso de direção muito ruim está caminhando para a frente e para trás no deserto. Inicialmente a iguana caminha 12 metros para a direita em um tempo de 20 segundos. A iguana então corre 16 metros para a esquerda em um tempo de 8 segundos.
Quais foram as velocidades escalar e vetorial médias da iguana para todo o trajeto?
Considere que a direita é a direção positiva. Para encontrar a velocidade escalar média dividimos a distância total percorrida pelo intervalo de tempo. velocidade escalar meˊdia=intervalo de tempo distancia percorrida=20,0 s+8,0 s12,0 m+16,0 {velocidade vetorial média}= {intervalo de tempo}}=velocidade vetorial meˊdia=intervalo de tempo deslocamento=28,0 s−4,0 {velocidade vetorial média}=-velocidade vetorial meˊdia=−71 s
Exemplo 2: O golfinho faminto
Um golfinho faminto está nadando para a frente e para trás na horizontal à procura de comida. O movimento do golfinho é dado pelo gráfico da posição mostrado abaixo.Determine o seguinte para o golfinho:
a. velocidade vetorial média entre t=0 \text{ s}t=0 st, equals, 0, start text, space, s, end text e t=6\text{ s}t=6 st, equals, 6, start text, space, s, end text
b. velocidade escalar média entre t=0 \text{ s}t=0 st, equals, 0, start text, space, s, end text e t=6\text{ s}t=6 st, equals, 6, start text, space, s, end text
c. velocidade vetorial instantânea em t=1\text{ s}t=1 st, equals, 1, start text, space, s, end text
d. velocidade escalar instantânea em t=4\text{ s}t=4 st, equals, 4, start text,
space, s, end text
Parte A: A velocidade vetorial média é definida como o deslocamento pelo tempo. a definição de velocidade vetorial média)}vmed=ΔtΔx=6 s−0 s 0 m−8 m= 6 s−8 m (use a definiça˜o de velocidade vetorial meˊ
Parte B: A velocidade escalar média é definida como a distância percorrida pelo tempo. A distância é a soma do comprimento do trajeto total percorrido pelo golfinho, então simplesmente somamos todas as distâncias percorridas pelo golfinho para cada parte do trajeto.v_{avg}=\dfrac{\text{distância percorrida}}{\Delta t}=\dfrac{12\text{ m}+0\text{ m}+4\text{ m}}{6 \text{ s}-0\text{ s}}=\dfrac{16\text{ m}}{6 \text{ s}}\quad\text{(use a definição de velocidade escalar média)}vavg=Δtdistaˆncia percorrida=6 s−0 s12 m+0 m+4 m=6 s16 m(use a definiça˜o de velocidade escalar meˊdia)
Parte C:A velocidade vetorial instantânea é a velocidade em um dado momento e será igual à inclinação do gráfico nesse momento. Para encontrar a inclinação em t=1\text{ s}t=1 st, equals, 1, start text, space, s, end text podemos determinar o “aumento pelo intervalo” para quaisquer dois pontos no gráfico entre t=0\text{ s}t=0 st, equals, 0, start text, space, s, end text e t=3\text{ s}t=3 st, equals, 3, start text, space, s, end text (já que a inclinação é constante entre esses tempos). Escolhendo os tempos t=2\text{ s}t=2 st, equals, 2, start text, space, s, end text e t=0\text{ s}t=0 st, equals, 0, start text, space, s, end text, encontramos a inclinação assim,v_\text{instantânea}=\text{inclinação}=\dfrac{x_2-x_0}{t_2-t_0}vinstantaˆnea=inclinaça˜o=t2−t0x2−x0v, start subscript, start text, i, n, s, t, a, n, t, a, with, \^, on top, n, e, a, end text, end subscript, equals, start text, i, n, c, l, i, n, a, ç, a, with, \~, on top, o, end text, equals, start fraction, x, start subscript, 2, end subscript, minus, x, start subscript, 0, end subscript, divided by, t, start subscript, 2, end subscript, minus, t, start subscript, 0, end subscript, end fractionv_\text{instantânea}=\dfrac{0\text{ m}-8\text{ m}}{2\text{ s}-0\text{ s}}=\dfrac{-8\text{ m}}{2\text{ s}}vinstantaˆnea=2 s−0 s0 m−8 m=2 s−8 mv, start subscript, start text, i, n, s, t, a, n, t, a, with, \^, on top, n, e, a, end text, end subscript, equals, start fraction, 0, start text, space, m, end text, minus, 8, start text, space, m, end text, divided by, 2, start text, space, s, end text, minus, 0, start text, space, s, end text, end fraction, equals, start fraction, minus, 8, start text, space, m, end text, divided by, 2, start text, space, s, end text, end fractionv_\text{instantânea}=-4\dfrac{\text{m}}{\text{s}}vinstantaˆnea=−4smv, start subscript, start text, i, n, s, t, a, n, t, a, with, \^, on top, n, e, a, end text, end subscript, equals, minus, 4, start fraction, start text, m, end text, divided by, start text, s, end text, end fraction[Como encontramos a velocidade vetorial instantânea?]Parte D:A velocidade escalar instantânea é a velocidade em um dado momento no tempo e é igual à magnitude da inclinação. Como a inclinação em t=4\text{ s}t=4 st, equals, 4, start text, space, s, end text é igual a zero, a velocidade escalar instantânea em t=4\text{ s}t=4 st, equals, 4, start text, space, s, end text também é igual a zero.


