Reflexão e Refração de Ondas
Reflexão de ondas
Quando uma onda sofre reflexão, a frequência, a velocidade de propagação e o comprimento de onda não variam.
Justificando:
Como a frequência depende somente da fonte, concluímos que a frequência da onda incidente é a mesma da onda refletida. A velocidade de propagação da onda depende do meio no qual ela se propaga. Na reflexão não há mudança de meio, logo a velocidade de propagação da onda incidente é a mesma da onda refletida. Não havendo mudança na frequência e na velocidade de propagação, resulta que o comprimento de onda também não varia.
Reflexão de um pulso que se propaga numa corda tensa
Vamos analisar dois casos:
1º Caso: reflexão em uma extremidade fixa
Considere uma corda AB com a extremidade B fixa em um ponto de uma parede rígida. Um pulso produzido na extremidade A, ao atingir o ponto B sofre reflexão e volta “invertido” em relação ao pulso incidente.
Neste caso, dizemos que a reflexão ocorreu com inversão de fase.
2º Caso: reflexão em uma extremidade livre
Podemos imaginar este caso considerando a extremidade B da corda presa a um anel que pode deslizar, sem atrito, ao longo de um eixo vertical. O pulso incidente atinge o ponto B e o anel sobe. Ao descer produz um pulso refletido “não invertido” em relação ao pulso incidente.
Nesta situação, dizemos que a reflexão ocorreu sem inversão de fase.
Refração de ondas
Quando uma onda sofre refração, a frequência não varia. A velocidade de propagação e o comprimento de onda variam no mesmo sentido, isto é, no meio onde a velocidade de propagação é maior o comprimento de onda também é maior.
Justificando:
Como a frequência depende somente da fonte, concluímos que a frequência da onda incidente é a mesma da onda refratada. A velocidade de propagação da onda depende do meio no qual ela se propaga. Na refração há mudança de meio, logo a velocidade de propagação da onda incidente é diferente da velocidade da onda refratada. De v = λ.f concluímos que o comprimento de onda da onda incidente é diferente do comprimento de onda da onda refratada.
Velocidade de propagação de uma onda transversal numa corda tensa
Considere uma corda de massa m e comprimento L e sob ação de uma força de tração de intensidade F.
Densidade linear da corda é a grandeza μ definida pela relação entre a massa m da corda e o seu comprimento L:
μ = m/L
A velocidade de propagação da onda na corda é dada pela raiz quadrada de F sobre μ:
v = √(F/μ)
Refração de um pulso que se propaga numa corda tensa
Considere o sistema constituído de duas cordas (1) e (2), de densidades lineares diferentes μ1 e μ2 com μ1 < μ2. Seja O o ponto de junção das cordas e F a intensidade da força de tração ao longo das cordas.
A extremidade B está fixa. O pulso produzido na extremidade A propaga-se na corda (1) com velocidade v1 = √(F/μ1).
Ao atingir a junção O, parte do pulso passa a se propagar na corda (2), isto é, ocorre refração do pulso. Na corda (2) a velocidade de propagação é
v2 = √(F/μ2) e sendo μ1 < μ2 resulta v1 > v2.
Na junção O, além da parte do pulso que se refrata, parte do pulso é refletido. O pulso refletido propaga-se com a mesma velocidade do pulso incidente. Observe que a reflexão ocorre com inversão de fase, pois o pulso incidente se propaga no sentido do meio (1) que é menos rígido para o meio (2), mais rígido.
Animação:
Clique aqui
Exercícios básicos
Exercício 1:
Assinale a proposição correta:
I) Na reflexão a frequência, a velocidade de propagação e o comprimento de onda não variam.
II) Na refração a frequência não varia. A velocidade de propagação e o comprimento de onda variam na mesma proporção.
III) A reflexão de um pulso pode ocorre com ou sem inversão de fase.
IV) A refração de um pulso ocorre sem inversão de fase.
Resolução: clique aqui
Exercício 2:
Um pulso é produzido na extremidade A de uma corda tensa, em duas situações mostradas nas figuras. Na primeira a extremidade B é fixa e na segunda livre.
Faça duas figuras representando o pulso refletido em cada situação.
Resolução: clique aqui
Exercício 3:
Considere o sistema constituído de duas cordas (1) e (2), de densidades lineares diferentes μ1 e μ2 com μ1 = μ2/4. Um pulso é produzido na extremidade A da corda tensa e na junção O sofre refração.
Determine a relação entre as velocidades de propagação v1/v2.
Resolução: clique aqui
Exercício 4:
Considere o sistema constituído de duas cordas (1) e (2), de densidades lineares diferentes, μ1 e μ2 com μ1 > μ2. O pulso produzido na extremidade A propaga-se na corda (1), atinge a junção O, e sofre refração e reflexão.
Faça uma figura representando os pulsos refratado e refletido.
Resolução: clique aqui
Exercício 5:
Um pulso com a forma indicada na figura abaixo é produzido na extremidade A de uma corda tensa, com a extremidade B fixa numa parede.
Das duas situações indicadas abaixo qual corresponde ao pulso refletido?
Resolução: clique aqui
Exercícios de Revisão
Revisão/Ex 1:
(FEI-SP)
As figuras representam dois pulsos que se propagam em duas cordas (I) e (II). Uma das extremidades da corda (I) é fixa e uma das extremidades da corda (II) é livre.

As formas dos pulsos reletidos em ambas as cordas, são respectivamente:



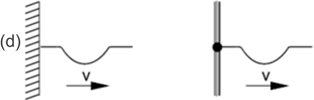
(e) Não há reflexão na corda (II)
Resolução: clique aqui
Revisão/Ex 2:
(UCBA)
O esquema representa um pulso que se propaga numa mola de extremidades fixas. A seta indica o sentido de propagação.

Dentre os esquemas a seguir o que representa o pulso refletido é:





Resolução: clique aqui
Revisão/Ex 3:
(UNB-DF)
O pulso assimétrico incidente de B para A (figura abaixo) deverá sofrer reflexão em A.

A configuração da corda após a reflexão será a figura:

a) I se a extremidade A for livre.
b) II se a extremidade A for livre.
c) III se a extremidade A for fixa.
d) IV se a extremidade A for fixa.
Resolução: clique aqui
Revisão/Ex 4:
(UC-GO)
A figura mostra o esquema composto por uma fonte de vibração ligada a duas cordas conectadas e tracionadas, uma corda PQ com densidade linear μ1 e a uma corda QR com densidade linear μ2 > μ1. Uma onda senoidal se propaga a partir da fonte com velocidade v1 = 15 m/s e comprimento de onda λ1 = 1,5 m na corda PQ. A onda continua a se propagar com uma velocidade v2 = 6 m/s na corda QR. Determine a frequência de vibração da fonte e o comprimento de onda na corda QR.

Resolução: clique aqui
Revisão/Ex 5:
(Mackenzie-SP)
A figura mostra uma onda transversal periódica, que se propaga com velocidade v1 = 8 m/s em uma corda AB, cuja densidade linear é μ1. Esta corda está ligada a uma outra BC, cuja densidade é μ2, sendo que a velocidade de propagação da onda nesta segunda corda é v2 = 10 m/s.

O comprimento de onda quando a onda se propaga na corda BC é igual a:
a) 7 m.
b) 6 m.
c) 5 m.
d) 4 m.
e) 3 m.
Resolução: clique aqui
n
Desafio:
Uma corda é feita de um material de densidade d = 5,0 kg/m3 e tem seção transversal de área A = 1,0.102 cm2. A corda está sendo tracionada, numa extremidade, por uma força de intensidade F = 2,0.10-3 N. A outra extremidade da corda efetua um MHS de frequência f = 4,0 Hz. Determine:
a) a densidade linear μ da corda;
b) a velocidade v de propagação das ondas na corda;
c) o comprimento de onda λ.
A resolução será publicada na próxima terça-feira
Resolução do desafio anterior:
Um bloco preso à extremidade de uma mola vertical, oscila realizando um movimento harmônico simples (MHS). O bloco é ligado a uma corda horizontal, homogênea e tensa, produzindo em 10 s o aspecto indicado abaixo. No instante representado, considere os pontos da corda indicados: 1, 2, 3 e 4. A distância entre os pontos 1 e 2 é de 8,0 cm.

a) Determine a frequência e a velocidade de propagação da onda na corda;
b) Dos pontos 1, 2, 3 e 4, quais têm módulo da velocidade máximo e quais têm módulo da velocidade nulo?
Resolução:
a) Da figura dada, concluímos que em 10 s, formam-se 2,5 ondas, isto é, são decorridos 2,5 T, onde T é o período:
2,5.T = 10 s => 2,5/f = 10 s => f = 0,25 s-1 => f = 0,25 Hz
A distância entre os pontos 1 e 2 corresponde a meio comprimento de onda: λ/2 = 8,0 cm => λ = 16 cm.
Velocidade da propagação da onda na corda
v = λ.f => v = 16cm.0,25s-1 => v = 4,0 cm/s
b) Os pontos da corda repetem o movimento da fonte, isto é realizam MHS vertical: ao passar pela posição de equilíbrio a velocidade tem módulo máximo e nos extremos de oscilação, o módulo da velocidade é nulo.
Assim:
pontos 1 e 2 => módulo da velocidade máximo,
pontos 3 e 4 => módulo da velocidade nulo.
Borges e Nicolau


