Atividade 5.1 – CINEMÁTICA

Habilidades: Identificar movimentos que se realizam no dia a dia e as grandezas relevantes que os caracterizam / Fazer estimativas, realizar ou interpretar medidas e escolher procedimentos para caracterizar deslocamentos, tempos de percurso e variações de velocidade em situações reais / Identificar diferentes formas de representar movimentos, como trajetórias, gráficos, funções etc.

SAEB Língua Portuguesa: D1 – Localizar informações explícitas em um texto

SAEB Matemática: D6 – Identificar a localização de pontos no plano cartesiano. / D14 – Identifica3r8 a localização de números reais na reta numérica / D20 – Analisar crescimento/decrescimento,  zeros de funções reais apresentadas em gráficos

A Cinemática é a parte da mecânica que estuda os movimentos dos corpos e das partículas. Ao contrário da dinâmica que estuda a causa dos movimento, a cinemática descreve o movimento de um corpo, mas não se preocupa com as suas causas. Seu estudo envolve as propriedades do movimento como posição, velocidade, aceleração, entre outras. Seu objeto de estudo é, sobretudo, os movimentos lineares e circulares.

Eles são divididos em Movimento Retilíneo Uniforme (M.R.U) e Movimento Retilíneo Uniformemente Variado (M.R.U.V).
O estudo do movimento de um corpo deve ser feito levando em consideração o seu comprimento, largura e altura. Nos casos em que essas dimensões são muito pequenas em relação ao percurso que esse corpo vai descrever, elas devem ser desprezadas e o corpo deve ser considerado como um ponto material.
Para entender melhor a cinemática, precisamos estar a par de variáveis como Deslocamento, Velocidade, Tempo e Aceleração. Esses conceitos são fundamentais para compreender alguns fenômenos físicos, bem como para a resolução de problemas matemáticos que envolvam suas fórmulas. 

Alguns conceitos de cinemática

Referencial, trajetória e deslocamento são alguns dos conceitos necessários para a correta compreensão da cinemática. Conheça essas variáveis e a fórmula matemática de algumas delas.

Partícula

A extensão do corpo (o tamanho) não é relevante e por isso não é levado em consideração.

Corpo extenso

As dimensões, ou seja, a extensão do corpo é levada em consideração.Os corpos são os objetos existentes em uma observação. Uma bola que realiza uma trajetória, por exemplo, é um corpo a ser considerado em uma análise cinemática. Os corpos podem ser materiais – quando suas dimensões não interferem no estudo de um determinado fenômeno físico; ou extensos – quando suas dimensões interferem na análise a ser realizada e precisa ser incluída no cálculo.

Normalmente representada pela letra S, nos informa o espaço percorrido pelo móvel. É bem simples, trata-se de uma subtração: onde o móvel chegou menos de onde o móvel saiu. Feito isto, teremos o resultado que nos informará a distância percorrida. (S – S0)

Posição

Normalmente representada pela letra S, nos informa o espaço percorrido pelo móvel. É bem simples, trata-se de uma subtração: onde o móvel chegou menos de onde o móvel saiu. Feito isto, teremos o resultado que nos informará a distância percorrida. (S – S0)

Referencial

É um ponto fixo pré-determinado, a partir do qual se pretende analisar se um corpo está ou não em movimento. O referencial é indispensável para se determinar a posição de um objeto. Seu conceito é adotado como o ponto de partida. Uma análise cinemática somente poderá ser feita com a definição de um referencial. Imagine um carro em movimento. Tomando como referencial a perspectiva do motorista, ele estará em repouso. Mas se o referencial for um ponto fixo de fora, ele estará em movimento.

Um corpo pode estar em movimento ou não dependendo da sua posição. Dentro de um elevador você está parado em relação ao próprio elevador, pois você não está se movimentando dentro dele.

Você agora, enquanto lê sobre o que é cinemática, sente-se parado em relação à terra, pois não está se movendo.  Mas em relação ao sol você está em movimento.

Por isso, para dizer se o móvel está ou não se movimentando, é preciso adotar um referencial, que nada mais é do que um ponto de vista. Logo, movimento e repouso são relativos! O que está em movimento para um observador pode estar em repouso para o outro e vice-versa.

Trajetória

É o caminho determinado por uma sucessão de pontos por onde o corpo passa em relação a certo referencial. O conceito de trajetória também é relativo. Isso ocorre porque referenciais diferentes podem ter visões diferentes do mesmo movimento. A trajetória é sequência de posições de um móvel em movimento no decorrer do tempo. Isso significa que um corpo em movimento define sua trajetória com o passar do tempo.
Elas podem ser de movimento retilíneo ou curvilíneo.
• Trajetória de movimento retilíneo – segue um caminho reto em relação à direção ou sentido.

• Trajetória de movimento curvilíneo – faz uma curva durante sua realização.

Deslocamento

Representa a distância entre a posição inicial e final, ou seja, é a variação da posição de um móvel sobre uma trajetória. Trata-se do espaço existente, em um intervalo de tempo definido, entre a posição inicial do corpo e sua posição final.
Dessa forma, o deslocamento é a variação da posição de um corpo. A função deslocamento pode ser calculada da seguinte maneira:

Movimento Uniforme 

Neste movimento a velocidade é constante, não muda, ou seja, tem sempre o mesmo valor durante todo o tempo de deslocamento! A fórmula é bem simples: A velocidade é igual à distância dividida pelo tempo. Pronto! Lembre-se, nas unidades certas como vimos acima

• V = D/T (Para facilitar usamos D como distância e ela é o cálculo da variação da posição S do móvel. Usamos T como tempo!)
• T = D/V (O tempo é igual à distância dividida pela velocidade.)
• T.V = D ( O tempo multiplicado pela velocidade é igual à distância.)

Função horária do MU: Ela é usada para informar em qual posição o móvel está em determinado tempo, basta substituir na fórmula as informações que você tem e descobrir a que não tem.

S = S0 + V.T

Obs: S = posição final e S0 = posição inicial

O movimento pode ser progressivo (a posição aumenta com a velocidade) ou retrógrado (a posição diminui com a velocidade).

Sobre o gráfico do MU: Em um gráfico onde um eixo informa a velocidade e o outro eixo informa o tempo a área formada pela figura te informa o espaço percorrido.

Em um gráfico onde um eixo informa a posição e o outro eixo informa o tempo, a inclinação da reta informa a velocidade. Precisamente, em um gráfico de posição x tempo, a tangente do ângulo de inclinação da reta representada é a velocidade.

Movimento Uniformemente Variado (M.U.V)

O Movimento Uniformemente Variado possui variação da velocidade ou seja, há uma grandeza física nesse movimento, chamada Aceleração. No M.U.V. o deslocamento aumenta ou diminui de acordo com a alteração das variáveis.

Função deslocamento 

Caminho percorrido

Além de analisar a posição final e inicial, essa variável analisa o espaço percorrido durante toda a trajetória. Essa diferença é mais fácil de compreender se imaginarmos uma trajetória curvilínea.
Se em uma trajetória retilínea um corpo se desloca 10 km em uma hora, o caminho percorrido também é de 10 km, uma vez que a trajetória não apresenta variações. No entanto, em uma trajetória curvilínea para deslocamento semelhante o caminho percorrido pode ser maior, a depender do desvio realizado.

Velocidade média

Grandeza que calcula a rapidez do deslocamento de um corpo em um espaço de tempo

Habilidades: 

Identificar movimentos que se realizam no dia a dia e as grandezas relevantes que os caracterizam / Fazer estimativas, realizar ou interpretar medidas e escolher procedimentos para caracterizar deslocamentos, tempos de percurso e variações de velocidade em situações reais / Identificar diferentes formas de representar movimentos, como trajetórias, gráficos, funções etc.
SAEB Matemática: D6 – Identificar a localização de pontos no plano cartesiano. / D14 – Identificar a localização de números reais na reta numérica / D20 – Analisar crescimento/decrescimento, zeros de funções reais apresentadas em gráficos

A velocidade média é a divisão entre o caminho percorrido e o intervalo de tempo necessário para percorrer o caminho. Parte da grandeza física que que identifica o deslocamento de um corpo em um determinado espaço de tempo, ela também é conhecida como velocidade escalar média.

Considerada a grandeza responsável por medir o quão rápido um objeto se desloca, a velocidade média é conceito usado pela cinemática para determinar a divisão entre o caminho percorrido e o intervalo de tempo necessário para percorrê-lo. Trata-se de um dos conceitos de cinemática, o ramo de estudo mecânica que analisa os movimentos dos corpos. Por isso, para compreender a velocidade média, é necessário entender alguns conceitos ligados à cinemática.

O velocímetro é usado para indicar a velocidade de um veículo. (Foto: Pixabay)

Velocidade

Velocidade é a grandeza vetorial que possui módulo, direção e sentido. Diretamente ligada à variação da posição, relaciona a distância percorrida por um corpo em um determinado intervalo temporal. 
O estudo da velocidade pode ser dividido em velocidade média e velocidade instantânea. A velocidade instantânea identifica a velocidade de um corpo em um momento específico, enquanto a velocidade média é o resultado da razão entre o espaço percorrido e o tempo gasto.

Embora seja uma grandeza vetorial, quando se refere a problemas simples, onde há deslocamento apenas em movimento unidimensional, a velocidade pode ser tratada como um grandeza escalar, ou seja, que possui apenas valor numérico. No entanto, vale salientar que velocidade escalar e velocidade vetorial possuem conceitos distintos. 

A velocidade vetorial é uma grandeza vetorial que mede o deslocamento (ou alteração na posição, Δs) sobre a alteração no tempo (Δt) representado pela equação

v = Δs/Δt.

A principal diferença entre elas é que a velocidade escalar não possui direção. Isso significa que se trata somente de uma medida escalar.

Por isso, quando se fala apenas em velocidade a referência é a escalar ou magnitude da velocidade vetorial e, não necessariamente, a velocidade vetorial. A velocidade escalar é uma grandeza escalar que mede a distância percorrida (d) sobre a alteração no tempo (Δt) representada pela equação

v = d/Δt.

https://youtube.com/watch?v=ooQyurVqT58%3Ffeature%3Doembed

Calculando a velocidade média

Para calcular a velocidade média que se conhece a variação do espaço percorrido, é preciso dividi-la pelo intervalo de tempo em que o movimento ocorreu. Esse intervalo de tempo é a diferença entre o instante inicial e o instante final.
A velocidade média de um corpo pode ser definida matematicamente pela equação a seguir:

Fórmula da velocidade média. 

Onde:
Vm: Velocidade Média
∆s: Intervalo do deslocamento posição final – posição inicial
∆t: Intervalo de tempo final – tempo inicial
Já para casos em que não se tenha conhecimento sobre o tempo ou o espaço, é possível descobri-los utilizando a fórmula a seguir:

Fórmula para encontrar o valor do tempo e do espaço.

Conversão da velocidade média (m/s para km/h)
A unidade de medida da velocidade adotada pelo Sistema Internacional de Unidades (SI) é dada em metros por segundo (m/s). Contudo, para escalas maiores, utiliza-se também quilômetros por hora (km/h). Nesse caso, importante destacar que é necessário converter m/s em km/h.
A conversão pode ser feita por meio do seguinte cálculo.

Esquema de conversão. (Foto: Educa Mais Brasil)
Na conversão de m/s para km/h é preciso multiplicar o valor por 3,6, já para transformar de km/h em m/s divide-se o valor por 3,6. O cálculo ocorre porque 1 km são 1000 metros e 1 hora corresponde a 3600 segundos.

Velocidade média e movimento

A velocidade média ocorre de maneira diferente e pode variar a depender do tipo de movimento. 

Movimento uniforme (MU): no MU o corpo se desloca mantendo a velocidade média constante igual a velocidade instantânea, portanto, não há aceleração. Movimento retilíneo uniforme (MRU): no MRU, além da velocidade constante, o corpo em movimento encontra-se em linha reta em relação ao referencial.

Movimento uniformemente variado (MUV): no MUV o corpo se movimenta com velocidades diferentes, variando de maneira uniforme, de modo que a velocidade média é diferente da velocidade instantânea. 

O termo Velocidade Média é usado pela cinemática como definição da divisão entre o caminho percorrido e o intervalo de tempo necessário para percorrer o caminho. A velocidade Média é o cálculo entre a distância percorrida por um corpo e o tempo gasto para percorrê-la.
A velocidade média pode ser definida matematicamente pela seguinte fórmula:

Fórmula da velocidade média

Velocidade escalar instantânea
A velocidade escalar instantânea pode ser explicada como a velocidade escalar média em um intervalo de tempo extremamente pequeno, ou seja, a um tempo próximo de zero. Desse modo, a velocidade escalar instantânea pode ser representada pela fórmula a seguir:

Fórmula da velocidade escalar instantânea

Aceleração escalar média

A aceleração escalar média está diretamente ligada à variação da velocidade de um corpo no decorrer do tempo. Assim, podemos definir aceleração de um móvel através da seguinte fórmula:

Fórmula da aceleração Aceleração escalar instantânea A aceleração escalar instantânea é a aceleração escalar média para um tempo muito pequeno, próximo de zero

Como resolver exercícios de Cinemática?

Confira algumas dicas para resolver uma boa parte dos exercícios de Cinemática:

1. Boa interpretação: A leitura é fundamental para a compreensão de um problema de Cinemática. Às vezes será necessário ler o exercício mais de uma vez para que se compreenda o problema totalmente. Com o tempo, você perceberá que algumas variáveis importantes dos exercícios estão implícitas no texto ou ainda em gráficos ou até mesmo em figuras. Veja exemplos:

Exemplo 1

Um corpo parte do repouso.

Nessa frase, fica implícito que a velocidade inicial do corpo era igual a 0 (v₀ = 0) e que ela sofreu alguma alteração, indicando a existência de uma aceleração. É possível inferir, nesse caso, que o seu movimento é uniformemente variável.

Exemplo 2

Um carro, movendo-se a 20 m/s, freia até parar completamente.

Analisando a frase, percebemos que a velocidade inicial do corpo era igual a 20 m/s (v₀ = 20 m/s) e que a velocidade final do carro é 0, pois ele para completamente (v_f = 0 m/s). Como sua velocidade inicial é positiva e diminui com o tempo, inferimos que ele se afasta do observador e ao mesmo tempo desacelera, tratando-se, portanto, de um movimento uniformemente variado, progressivo e retardado.

2. Sempre anote os dados do exercício:

Sempre anote todas as variáveis que o exercício fornece, bem como todas aquelas que ele pede que você calcule ou que não tenham sido informadas, mas que sejam importantes para a solução do problema. Veja um exemplo:

Um motorista, dirigindo em uma estrada a 108 km/h, avista uma placa de pare e então aciona os freios do seu veículo, parando totalmente 6 s após o início da frenagem. Calcule o módulo da aceleração média, em m/s², sofrida pelo veículo a partir da frenagem.

Dados:

v₀ = 108 km/h – velocidade inicial
v_f = 0 m/s – velocidade final
Δt = 6 s – intervalo de tempo
a_m = ? – aceleração média (incógnita)

Resposta:

a = -5m/s²

Explicação:

Note que, temos uma incompatibilidade de unidades e, portanto, devemos converter os 108 km/h em m/s dividindo por 3,6.

V = 108km/h

Divide por 3,6

V = 108/3,6 = 30m/s

A aceleração é igual

a = ΔV/ΔT

ΔV é a variação da velocidade, sendo velocidade final menos velocidade inicial (V – Vi

a = V – Vi/ΔT

Como a velocidade final é igual a 0 (V=0)

a = 0 – 30/6

a = -5m/s²

3. Confira as unidades: As unidades devem ser sempre compatíveis entre si, isto é, devem estar todas representadas no mesmo sistema de unidades. O Sistema Internacional de Unidades utiliza o padrão metro e segundo para distâncias e intervalos de tempo, respectivamente. Dessa forma, a velocidade deve ser dada em m/s. Confira algumas transformações úteis:

1 quilômetro = 1 km = 10³ m = 1000 m

1 centímetro = 1 cm = 10^-2 m = 0,01 m

1 quilômetro por hora = 1 km/h = 3,6 m/s (metros por segundo)

1 milha = 1,60934 km

1 milha por hora = 1 mph = 0,44704 m/s (metros por segundo)

4. Conheça as equações do movimento: O movimento uniforme, isto é, o movimento sem aceleração, só tem uma equação. Já o movimento acelerado apresenta quatro equações que podem ser usadas em situações diferentes. Confira:

Velocidade média: É a equação usada para o movimento uniforme, isto é, o movimento cuja velocidade é constante. Nesse tipo de movimento, o corpo desloca-se espaços iguais em intervalos de tempo iguais. Veja a mesma equação escrita de duas formas diferentes:

v_m = ΔS
         Δt

  ou

   S_f = S₀ + v_m.t

Legenda:

S₀ = Posição inicial
S_f = Posição final
ΔS = S_f – S₀ – Deslocamento
v = Velocidade média
Δt = Intervalo de tempo

Aceleração média: É a equação usada para o movimento uniformemente variado, isto é, o movimento cuja velocidade varia de forma constante. Nesse tipo de movimento, o corpo tem sua velocidade alterada em proporções iguais durante intervalos de tempo iguais. Veja a mesma equação escrita de duas formas diferentes:

A_m = Δv
         Δt

ou

v_f = v₀ + A_m.t

Legenda:

v₀ = Velocidade inicial
v_f = Velocidade final
Δv = v_f – v₀ – Variação da velocidade
A_m = Aceleração média
Δt = Intervalo de tempo

Função horária da posição: Essa é a equação utilizada quando precisamos descobrir o deslocamento ou a posição final e inicial de um móvel que se move com aceleração constante. Veja a mesma equação escrita de duas formas distintas:

ΔS = v₀.t + A_m.t²
                      2

S_f = S₀ + v₀.t + A_m.t²
                             2

Legenda:

S₀ = Posição inicial
S_f = Posição final
ΔS = S_f – S₀ – Deslocamento
v₀ = Velocidade inicial
A_m = Aceleração média
Δt = intervalo de tempo

Equação de Torricelli: Essa equação tem uso parecido com o da equação mostrada anteriormente, no entanto, pode ser muito útil quando o enunciado do exercício não informa o tempo em que o movimento ocorreu. Observe:
 

v_f ²= v₀² + 2.A_m.ΔS

Legenda:

v_f = velocidade final
ΔS = S_f – S₀ – deslocamento
v₀ = velocidade inicial
A_m = aceleração média

É possível verificar os gráficos no próprio
simulador.

2. Comece a simulação colocando o homem na posição S0 = 0m da trajetória, velocidade v = 2 m/s, aceleração 1 m/s2 e responda:
   a) O movimento é progressivo ou retrógrado? Acelerado ou retardado? Justifique sua resposta.
   Progressivo, pois o deslocamento se dá no sentido adotado como positivo na trajetória e acelerado, pois a velocidade aumenta com o decorrer do tempo, lembrando que o valor da aceleração é positivo, o que caracteriza
   o tipo de movimento.
   b) Classifique o movimento em Movimento Retilíneo Uniforme (MRU) ou em Movimento Retilíneo Uniformemente Variado (MRUV)
   MRUV, pois o homem percorreu uma trajetória retilínea com aceleração constante e maior que zero.
   c) Qual a posição do homem após 3s? Comprove utilizando a equação da função horária da posição
   S(t) = S₀ + v . t + a . t² /2
   Antes de realizar o cálculo, faça o teste no simulador. O cálculo servirá para comprovar o resultado. Então, será
   possível explicar a utilização da fórmula.
   S(t) = 0 + 2 . 3 + 1. 3²/2
   S(t) = 6 +1.9/2
   S(t) = 6 + 4,5
   S(t) = 10,5 m
   d) Represente o gráfico s (y) x t (x).

É possível verificar os gráficos no próprio simulador.
e) Represente o gráfico v (y) x t (x).

É possível verificar os gráficos no próprio simulador.

1. Use a função horária da velocidade!

v = v₀ + a.t

Legenda:
v = velocidade final
v₀ = velocidade inicial
a = aceleração
t = instante de tempo

Use essa função quando:

• Você souber o valor da velocidade inicial (v₀), da aceleração (a) e do tempo (t) e quiser calcular a velocidade final (v);
• Você souber o valor da velocidade inicial (v₀), da aceleração (a), da velocidade final (v) e quiser calcular o tempo (t);
• Você souber o valor da velocidade inicial (v₀), da velocidade final (v), do tempo (t), mas quiser calcular a aceleração (a);
• Você souber o valor da velocidade final (v), da aceleração (a) e do tempo (t), mas quiser calcular o valor da velocidade inicial (v₀).

Obs.: Com essa equação, não é possível calcular o deslocamento (ΔS).

Resolva alguns exercícios: Exercícios sobre aceleração média

2. Use a equação de Torricelli!

v² = v₀²+ 2.a.ΔS

Legenda:
v = velocidade final
v₀ = velocidade inicial
a = aceleração
ΔS = deslocamento

Use essa função quando:

• Você souber o valor da velocidade inicial (v₀), da velocidade final (v), da aceleração (a) e quiser calcular o deslocamento (ΔS);
• Você souber o valor da velocidade inicial (v₀), da velocidade final (v), do deslocamento (ΔS) e quiser calcular a aceleração (a);
• Você souber o valor da velocidade inicial (v₀), da aceleração (a), do deslocamento (ΔS) e quiser calcular o valor da velocidade final (v);
• Você souber o valor da velocidade final, da aceleração (a), do deslocamento (ΔS) e quiser calcular o valor da velocidade inicial (v₀).

Obs.: Com essa equação, não é possível calcular o tempo (t).

Resolva alguns exercícios: Exercícios sobre equação de Torricelli
 

3. Use a equação da média das velocidades!

ΔS = (v + v₀).t
         2

Legenda:
v = velocidade final
v₀ = velocidade inicial
a = aceleração
ΔS = deslocamento
t = instante de tempo

Use essa função quando:

• Você souber o valor do deslocamento (ΔS), da velocidade inicial (v₀), da velocidade final (v), mas não souber o instante de tempo (t);
• Você souber o valor do deslocamento (ΔS), da velocidade inicial (v₀), do instante de tempo (t), mas não souber a velocidade final (v);
• Você souber o valor do deslocamento (ΔS), da velocidade final (v), do instante de tempo (t), mas não souber o valor da velocidade inicial (v₀);
• Você souber o valor da velocidade final (v), da velocidade inicial (v₀), do instante de tempo (t), mas não souber o deslocamento (ΔS).

Obs.: Com essa equação, não é possível calcular a aceleração (a).

Veja também: Dicas para resolver exercícios de Física
 

4. Use a função horária da posição!

ΔS = v₀.t + a.t²
​​​​                   2

Legenda:
v₀ = velocidade inicial
a = aceleração
ΔS = deslocamento
t = instante de tempo

Use essa função quando:

• Você souber o valor do deslocamento (ΔS), da velocidade inicial (v₀), da aceleração (a), mas não souber o instante de tempo (t);
• Você souber o valor do deslocamento (ΔS), da velocidade inicial (v₀), do tempo (t), mas não souber o valor da aceleração (a);
• Você souber o valor do deslocamento (ΔS), da aceleração, do tempo (t), mas não souber o valor da velocidade inicial (v₀);
• Se você souber o valor da aceleração (a), do tempo (t), da velocidade inicial (v₀), mas não souber o valor do deslocamento (ΔS).

Obs.: Com essa equação, não é possível calcular a velocidade final (v).

Se você estiver resolvendo algum exercício e perceber que duas variáveis estão faltando, você pode usar duas das fórmulas acima, descobrindo cada uma dessas variáveis por vez. Para cada fórmula acima, admite-se que falte apenas uma variável, que será a sua incógnita. Para resolver a equação, você deve sempre isolá-la.

Veja também: Macetes para fórmulas de Física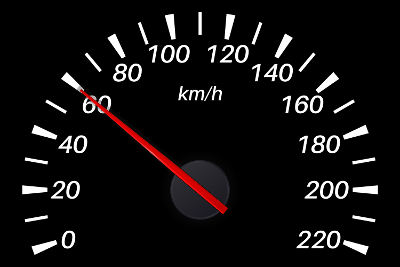
O velocímetro mostrado acima indica que o veículo desloca-se 60 km a cada hora, em relação ao solo

Postado por Fabiana Dias em 03/12/2018 e atualizado pela última vez em 17/07/2020