Porcentagem: Aplicações Com Exercícios
Porcentagem ou percentagem é usada para calcular descontos, acréscimo de preços, lucros, etc. É uma fração em que o denominador é igual a 100. O símbolo para representar uma porcentagem é % e vem precedido por um número.
Definição
Ao número p associamos a razão p⁄100, ou seja, tomamos p partes de um todo que foi dividido em 100 partes iguais.
Exemplo: 5% (leia-se: cinco por cento) equivale a fração 5⁄100.
O nome tem origem do latim (per centum) e quer dizer por cento, ou seja, uma razão de base 100. É frequentemente utilizado para cálculos de transações comerciais, entre outros.
Essas razões com denominadores 100 são chamadas de razões centesimais, taxas percentuais ou, simplesmente, porcentagens.
Porcentagem no dia a dia
Um dos assuntos que caem em vestibulares, dos mais concorridos aos menos concorridos do país, também aparece frequentemente em questões do ENEM.
Além disso, sempre vimos nos telejornais notícias relacionadas, por exemplo: “O preço da gasolina aumentou 10%”. Dessa forma, se a gasolina custa 5,00 reais e esta irá sofrer um reajuste (aumento) de 10%, na matemática escreveremos assim:
10% de 5,00 = 10⁄100 . 5 = 0,50
Ou seja, a gasolina sofrerá um aumento de 50 centavos por litro.
Ao calcularmos uma porcentagem em relação a um valor dado, estamos também representando uma proporção em que um dos denominadores é igual a 100.
Pelo exemplo acima dado, dizemos que 0,50 representa em 5 o mesmo que 10 representa em 100. Veja:
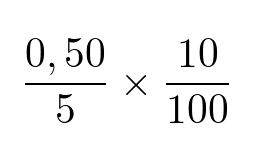
Como representar porcentagem?
Existem três formas de representarmos uma porcentagem: na forma percentual, forma fracionária ou forma decimal. Veja:
| Forma percentual | Forma fracionário | Forma decimal |
|---|---|---|
| 10% | 10⁄100 | 0,1 |
| 30% | 30⁄100 | 0,30 |
| 5,3% | 5,3/100 | 0,053 |
Podemos perceber como a porcentagem está presente na nossa vida. Descontos em lojas, promoções na internet, dificilmente você vai se livrar do assunto.
Usamos a porcentagem quando queremos expressar alguma quantidade como a porcentagem de um valor. Veja um exemplo:
Digamos que você vai em uma loja no shopping ou numa loja virtual na internet e encontre um produto com desconto de 10%. Seu custo inicial era de R$ 50,00. Esse desconto de 10% corresponde à divisão do preço inicial por 100, tomando 10 partes. Veja:
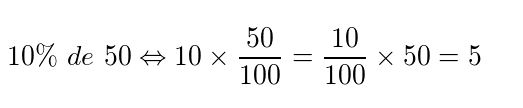
Resumindo: calcular a porcentagem de a% de x é o mesmo que multiplicar a/100 por x.
Entender porcentagem é fundamental para o dia a dia. Se você for a um posto de combustível abastecer seu carro, após ouvi na televisão que a gasolina teve tantos por cento de aumento e, digamos que seu carro seja flex, então você para e pensa: “devo abastecer com álcool ou gasolina? Quantos por cento devo abastecer de álcool ou gasolina?”.
São problemas como esse que nos deparamos e percebemos que a porcentagem é muito importante em nossa vida.
Exercícios de porcentagem
Calcule 20% de 500
20% é o mesmo que escrevermos 20/100 20% de 500 =
Coloque 5⁄4 na forma percentual.
Essa é uma forma de conversão mais completa, aqui usamos regra de três. Pegamos o valor que queremos converter (5⁄4), depois colocamos o valor que não sabemos na base 100 ( x/100 ).
Próximo passo é usar a regra de três para encontrar o valor de x. Então multiplicaremos a proporção em cruz.
Após encontrar o valor de x, colocamos o valor que queremos na base 100. Ou seja, reescrevermos, pois queremos na forma percentual, colocando o símbolo.
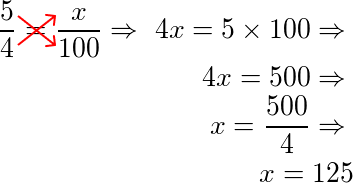
Logo,
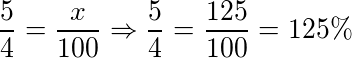
Coloque 3⁄4 na forma percentual.
Essa forma que vamos ensinar é mais rápida e prática.
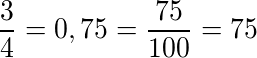
Basta dividir a fração, encontramos um valor na forma decimal (com vírgula), deslocamos a vírgula duas casas para a direita e para converter na forma percentual colocamos o valor encontrado na base 100 ou 75%.
Coloque 7⁄5 na forma percentual.
Dividimos 7 por 5, deslocamos a vírgula para a direita duas casas, colocamos o valor na base 100 ou 140%.
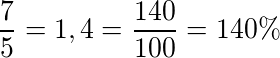
Colocar 30% na forma decimal
Aqui basta reescrever a porcentagem sem usar o símbolo %, colocar na base 100; e para colocar na forma decimal, dividimos o valor pelo 100.
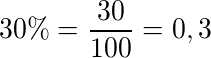
- Responda os exercícios propostos
Porcentagem e regra de três simples
Grande parte dos problemas envolvendo porcentagem podemos resolver aplicando regra de três simples.
Chamamos de regra de três simples quando um problema têm três valores conhecidos e queremos encontrar um valor desconhecido que resolve o problema.
Técnica operatória
A técnica para resolver porcentagem por regra de três é a seguinte:
| Grandeza % (ou ‰) | Grandeza do problema |
|---|---|
| 100 (ou 1000) | P |
| i | p’ |
Separando as grandezas, armamos o problema e conseguimos resolver por regra de três.
Exemplo: calcule 40% de 80.
Montando o problema, temos:
100% corresponde a 80
40% corresponde a x
x é o valor que queremos encontrar.
Então:
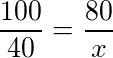
Multiplicando em cruz, temos,
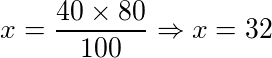
Portanto, 40% de 80 é igual a 32.
Porcentagem e lucro
Imagine que você comprou um imóvel por R$ 10.000,00 e alguns anos depois vendeu este imóvel por R$ 26.350,00. Qual o lucro, em porcentagem, que você obteve com a venda do imóvel?
Bem fácil observar que o lucro neste caso foi de R$ 16.350,00.
Ou seja, 26.350,00 – 10.000,00 = 16.350,00
Mas queremos saber o quanto você obteve de lucro em porcentagem.
Dessa forma, dividimos o lucro (R$ 16.350,00) pelo valor de compra do imóvel (R$ 10.000,00) e multiplicamos o resultado por 100. Veja:
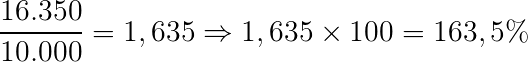
Assim, seu lucro em porcentagem foi de 163,5%.
- Responda os exercícios sobre porcentagem
Porcentagem e desconto
Ao comprar um produto numa loja virtual ou loja física você encontra uma promoção de 10%. Suponha que este produto seja uma calça jeans no valor de R$ 250,00. Qual o preço após o desconto obtido?
Para saber o desconto obtido, em reais, temos que multiplicar o desconto em porcentagem pelo valor da calça. Veja:
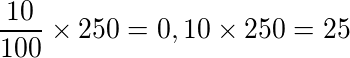
Assim, você obteve um desconto de R$ 25,00 no valor final do produto. Então, o preço após aplicar o desconto é: 250,00 – 25,00 = 225,00
Você comprou o calça jeans por R$ 225,00.
- Veja os exercícios propostos
Porcentagem e acréscimo (reajuste)
O governo informa que a conta de luz sofrerá um acréscimo (reajuste) de 8%. Caso a conta de luz de um morador seja de R$ 120,00 mensais, quanto será o aumento total na conta de luz para este morador?
Preço da conta de luz, hoje: R$ 120,00
Cálculo do acréscimo (reajuste):

Assim, a conta de luz desse morador terá um reajuste de R$ 9,60. Então, após aplicarmos o reajuste ele pagará: 120 + 9,6 = 129,6.
A conta de luz passará a custar R$ 129,60.
- Confira os exercícios propostos
Porcentagem e razão
Em uma sala de aula, a razão de alunos entre o número de mulheres e o de homens é 2⁄5. Qual a porcentagem de alunas nessa sala em relação ao total de alunos da sala?
Vamos atribuir a variável x para as mulheres e y para os homens. Não sabemos nem o total de homens nem o total de mulheres nessa sala. Temos:
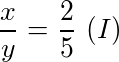
Para saber o total de
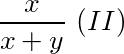
ou seja, o total de mulheres é a quantidade de mulheres x sobre o total de alunos, mulheres e homens (x + y).
Vamos calcular (I):
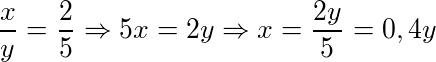
Substituindo em (II):

Então, a porcentagem de mulheres na sala de aula é: 28,57%.
Exercícios
Confira alguns exercícios para responder no link abaixo:
Bom, aprendemos um pouco sobre porcentagem que você pode aplicar no dia a dia.
Leia também
Exercícios de Porcentagem, Com Gabarito
Página Inicial » Matemática Financeira » Exercícios de Porcentagem, Com Gabarito
Exercícios propostos sobre porcentagem para fixar o aprendizado sobre esse tema tão importante.1) Um artigo esportivo teve um aumento de 20%, e agora custa R$ 180,00. Qual era o preço antes desse aumento?Ver resposta2) Uma loja vendia uma TV por R$ 2.000,00. No dia das mães, a loja anunciou uma promoção oferecendo 20% de desconto em todos os produtos do estoque. Qual o preço final da TV depois do desconto?Ver resposta3) Se 40% de um número qualquer é 20, determine esse número.Ver resposta4) (OBMEP – 06) Um trabalho de matemática tem 30 questões de aritmética e 50 de geometria. Júlia acertou 70% das questões de aritmética e 80% do total de questões. Qual o percentual das questões de geometria que ela acertou?Ver resposta5) Numa padaria, 60 kg de farinha e fermento, 2% é de fermento. Se acrescentarmos mais 100 gramas de fermento, qual a porcentagem da nova mistura?Ver resposta
Encontrou algum erro? Nos a


