Habilidades: Reconhecer causas da variação de movimentos associadas a forças e ao tempo de duração das interações. / Identificar as interações nas formas de controle das alterações do movimento. / Reconhecer a conservação da quantidade de movimento, a partir da observação, análise e experimentação de situações concretas, como quedas, colisões, jogos ou movimentos de automóveis. / Comparar modelos explicativos das variações no movimento pelas leis de Newton / Reconhecer que tanto as leis de conservação das quantidades de movimento como as leis de Newton determinam valores e características dos movimentos em sistemas físicos.
SAEB Língua Portuguesa: D1 – Localizar informações explícitas em um texto / D3 – Inferir o sentido de uma palavra ou expressão / D4 – Inferir uma informação implícita em um texto / D6 – Identificar o tema de um texto / D14 – Distinguir um fato da opinião relativa a esse fato / D21 – Reconhecer posições distintas entre duas ou mais opiniões relativas ao mesmo fato ou ao mesmo
Está aí a relação matemática que considero a mais traiçoeira entre todas as estudadas a nível de ensino médio. A segunda lei de Newton diz respeito sobre a proporção entre uma força resultante e a aceleração por ela produzida no corpo. Em módulo:
FR = ma
Em termos vetoriais, dizemos que o vetor força resultante é de mesma direção e sentido que o vetor aceleração por ele produzido. E como isto pode enganar alguém? Se basta ter dois deles para efetuar a operação matemática e então achar o terceiro…
Aí é que está, existem casos e casos os mais variados possíveis nos quais a força resultante sobre um corpo ou um conjunto de corpos será diferente em cada um deles. Fazendo com que a segunda lei se desdobre em inúmeras outras relações matemáticas.
A segunda lei de Newton, também conhecida como princípio fundamental da dinâmica, trata da relação entre a força e a aceleração de um corpo.
Essa é a segunda das três leis de Isaac Newton, que explicam a dinâmica do movimento dos corpos. As 1ª, 2ª e 3ª leis de Newton foram publicadas em 1687, no livro chamado Princípios Matemáticos da Filosofia Natural.
Essa é a única lei de Newton que pode ser representada por uma equação, onde a força resultante(Fr) é igual ao produto da massa(m) pela aceleração(a).
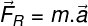
Explicação da 2ª lei de Newton
Segundo essa lei, para que um corpo ganhe aceleração e tenha sua velocidade alterada, é preciso que uma força seja aplicada sobre ele. A segunda lei, portanto, trata dos casos em que há aceleração na movimentação dos corpos, diferenciando-se da primeira lei, que trata dos casos em que a aceleração é nula.
Saiba mais sobre a primeira lei de Newton e terceira lei de Newton.
Para que um corpo saia do seu estado de equilíbrio e ganhe aceleração, a força resultante aplicada sobre ele deve ser diferente de zero.
Isso quer dizer que, se houver mais de uma força exercida sobre o corpo, é preciso fazer o somatório de todas as forças, pois essas forças poderão se intensificar se tiverem mesma direção e sentido, ou podem se anular, se tiverem sentidos opostos, por exemplo.
Veja a equação desta lei:
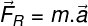
A partir dessa relação observamos que a força resultante pode ser calculada pela multiplicação da massa do corpo pela aceleração. Pela fórmula, constatamos também que força e massa são grandezas diretamente proporcionais.
Isso significa que, quanto maior a massa, maior deverá ser a intensidade da força para que o corpo ganhe aceleração. Isso acontece devido à inércia do corpo, que é sua tendência em permanecer no seu estado de equilíbrio.
A massa é a medida quantitativa da inércia, assim, quanto maior a massa, maior a inércia de um corpo. Veja este exemplo:
- Sobre uma superfície plana estão duas caixas de madeira, uma delas pesa 5 kg, a outra 500 kg. Caso uma pessoa tente empurrar essas caixas, ela terá muito mais facilidade em movimentar a caixa mais leve, pois sua massa é menor e, portanto, sua inércia também é menor.
Por outro lado, podemos observar que a massa e a aceleração são grandezas inversamente proporcionais. Isso porque, quanto maior a massa de um corpo, maior será sua resistência para mudar de velocidade e portanto, menor sua aceleração.
Para ficar mais clara essa relação, veja este exemplo:
Considere dois corpos com massas diferentes, o corpo A tem massa igual a 10 kg e o corpo B tem massa de 5 kg e sobre ambos os corpos é aplicada uma força de mesma intensidade.
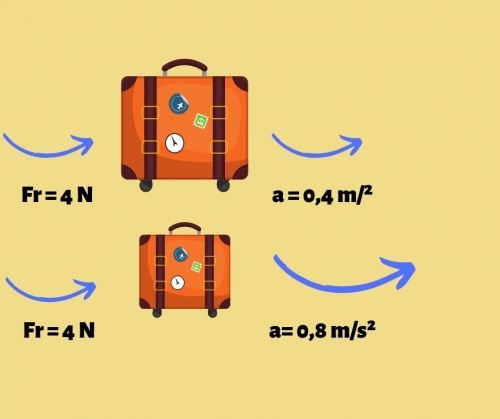
Ao aplicar a mesma força, o corpo de menor massa ganhou mais aceleração.
Nesse caso, o corpo B ganhará uma aceleração maior do que o corpo A. Isso acontece porque a massa do corpo B é menor e, portanto, sua resistência em aumentar de velocidade é menor.
As unidade de medida dessas grandezas são:
- Força (F) – Newton
- Massa (m) – kg
- Aceleração (a) – m/s²
Veja também o significado de inércia e força.
Agora que você já entendeu o que é a segunda lei de Newton, veja o exemplo de um exercício prático.
- Considerando dois corpos A e B, ambos com 100 kg. Sobre o corpo A é aplicada uma força de 40 newtons e sobre o corpo B é aplicada uma força de 60 newtons. Qual é a aceleração adquirida por cada um dos corpos?
Utilizando a fórmula:
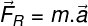
| Corpo A | Corpo B |
| 40 = 100.a a= 40/100 a= 0,4 m/s² | 60 = 100.a a = 60/100 a = 0,6 m/s² |
Como resultado, temos que a aceleração do corpo B é maior do que a aceleração do corpo A. Como ambos tem a mesma massa, a aceleração foi maior no caso em que a força resultante aplicada sobre o corpo foi mais intensa.
Para o mais simples dos casos temos a seguinte figura:
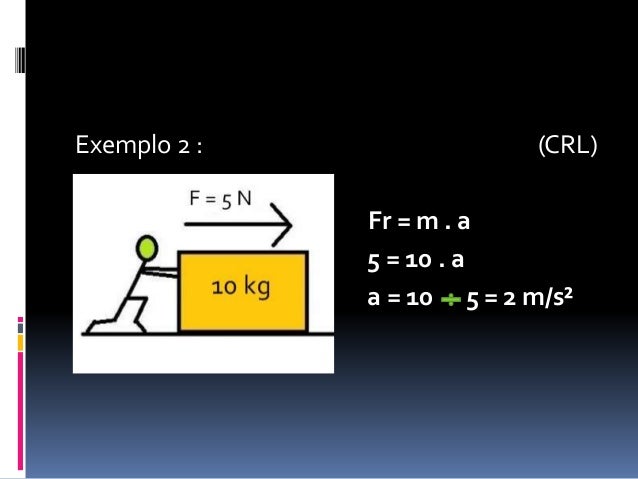
Analisando a imagem acima aos olhos da segunda lei temos que:
¬ quanto maior for a massa do corpo, para um força resultante de módulo constante, menor será o módulo da aceleração, pois massa e aceleração são inversamente proporcionais;
Exemplo: se empurramos horizontalmente para a direita com um força de 50 N dois corpos A e B de massas 5 Kg e 10 Kg as acelerações por eles adquiridas serão 10 m/s² e 5 m/s², , respectivamente.
¬ quanto maior for o módulo a força resultante sofrida, para corpos de massas iguais, maior será o módulo da aceleração adquirida, pois aceleração e força são diretamente proporcionais.
Exemplo: se empurrarmos, horizontalmente para a direita, um mesmo corpo de massa 5 Kg, com forças de módulos 10 N e 5 N, as acelerações adquiridas serão, respectivamente, iguais a 2 m/s² e 1 m/s².
Como resolver exercícios sobre as leis de Newton?
Para resolver exercícios sobre as aplicações das Leis de Newton, como em sistemas de blocos, é interessante seguir algumas etapas:
1. Anote todos os dados relevantes do enunciado;
2. Verifique se as unidades encontram-se no Sistema Internacional de Unidades (metro, quilograma e segundo);
3. Desenhe atentamente todas as forças que atuam sobre os corpos;
4. Tente perceber em qual direção o sistema de corpos move-se e adote o seu sentido para o sinal positivo das forças. Todas as forças que estiverem nesse sentido também serão positivas. As forças contrárias serão negativas;
5. Iguale a resultante das forças de cada corpo para cada direção do espaço ao produto m.a ou a 0, no caso em que o corpo estiver movendo-se com velocidade constante ou estiver em repouso;
6. Lembre-se de que corpos que se movem juntos, ligados por cabos, um em cima do outro ou ainda encostados são solidários e, portanto, apresentam a mesma aceleração;
7. Para resolver o sistema de equações, nós devemos subtrair uma pela outra, pois os pares de ação e reação têm o mesmo valor e cancelam-se.
Se você seguir atentamente a todos os passos acima, dificilmente cometerá algum erro ao resolver exercícios sobre as Leis de Newton.
Veja também: Cinco coisas que você precisa saber sobre as leis de Newton
Exercícios resolvidos sobre Leis de Newton
OBS.: Para todos os exemplos abaixo adotaremos a gravidade como 10 m/s².
Questão 1
Dois blocos, A e B, de massas iguais a 8 kg e 2 kg, respectivamente, estão representados na figura abaixo. Os blocos são unidos por um fio inextensível e puxados por uma força F de módulo igual a 20 N. Determine:
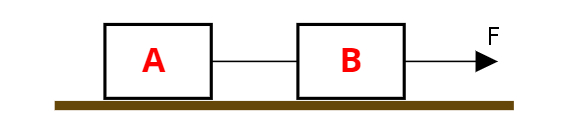
a) Aceleração do sistema
b) Tração no fio
Resolução:
1- Anotando os dados
Os dados mais relevantes do exercício são:
ma = 2 kg;
mb = 8 kg;
|F| = 20 N.
2 – Verificando as unidades
Todas as unidades são compatíveis entre si e estão no Sistema Internacional de Unidades;
3 – Fazendo o diagrama de forças
Desenheatentamente todas as forças que atuam em cada bloco. Devemos lembrar a força peso, força normal, tração no fio que o bloco A exerce sobre o bloco B e a força F que é aplicada sobre o bloco B. Ficamos com o seguinte esquema:
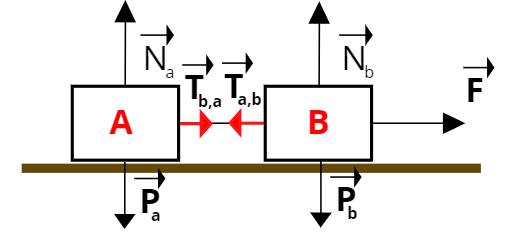
Legenda:
Pa = Peso do bloco A
Pb = Peso do bloco B
Na = Normal do bloco A
Nb = Normal do bloco B
F = Força sobre o sistema
Tb,a = Tração que o bloco B faz no bloco A
T a,b = Tração que o bloco A faz no bloco B
4 – Orientando o sistema de coordenadas
O sistema de blocos move-se para a direita e, portanto, todas as forças que apontam nesse sentido terão sinal positivo. As forças que apontam para a esquerda terão sinal negativo.
5 – Achando as forças resultantes
De acordo com o sinal adotado no passo 4, as forças resultantes, nas direções x e y (horizontal e vertical), para cada bloco serão determinadas por:
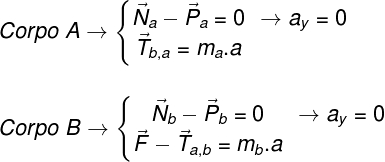
6 – Os corpos movem-se juntos
Perceba que a força normal e o peso de cada bloco cancelam-se, pois os blocos não se movem na direção y (vertical), logo, N = P. Além disso, como os blocos movem-se juntos, eles apresentam o mesmo valor de aceleração.
7 – Resolvendo o sistema de equações
Para resolver o sistema de equações, vamos atribuir ao sistema de equações encontrado no passo 5 os valores que anotamos no passo 1. Lembre-se de que o peso dos corpos é dado por m.g (massa vezes gravidade):
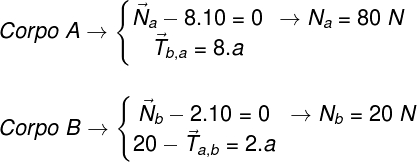
A tração que o corpo B faz no corpo A e a tração que o corpo A faz no corpo B são um par de ação e reação, portanto, se somarmos as equações, esses termos (Ta,b e Tb,a) devem cancelar-se. Fazendo isso, ficamos somente com:
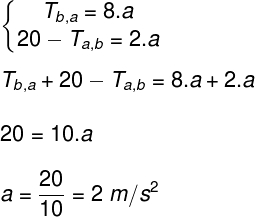
Para determinar a tração no fio, tanto faz calcularmos o módulo de Ta,b ou de Tb,a, uma vez que as duas forças são um par de ação e reação, logo, possuem o mesmo módulo:
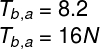
A tração exercida pelo fio é de 16 N.
Veja também: Sete erros mais comuns cometidos no estudo de Física
Questão 2
Dois blocos, A e B, de massas iguais a 7 kg e 3 kg são ligados por um fio inextensível como mostra a figura abaixo. Calcule a aceleração do sistema e a tração nos dois fios.
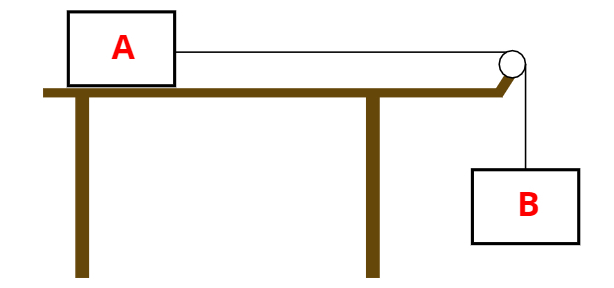
Resolução:
1 – Anotando os dados
Os dados relevantes do exercício são:
ma = 7 kg
mb = 3 kg
g = 10 m/s²
2 – Verificando as unidades
Todas as unidades são compatíveis entre si e estão no Sistema Internacional de Unidades.
3 – Fazendo o diagrama de forças
Vamos desenhar todas as forças presentes nos blocos. Observe a figura abaixo:
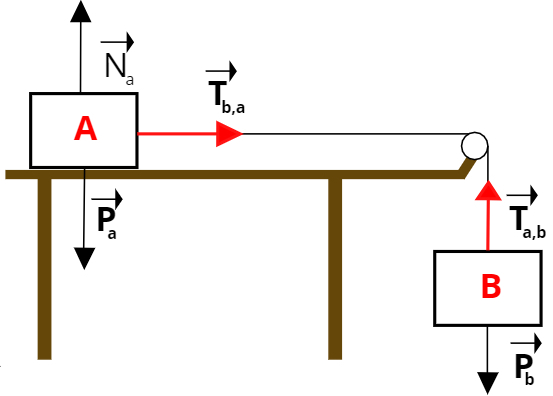
Perceba que como o corpo B não está apoiado sobre a mesa, não há força normal sobre ele.
4 – Orientando o sistema de coordenadas
Os blocos movem-se em direções perpendiculares. O bloco A move-se na direção x para a direita, então, todas as forças sobre esse bloco que apontem para a direita serão positivas. O bloco B move-se na direção vertical para baixo, logo, todas as forças sobre esse bloco que apontem para baixo serão positivas.
5 – Achando as forças resultantes
O sistema de equações fornecido pelas forças resultantes dos blocos é apresentado a seguir:
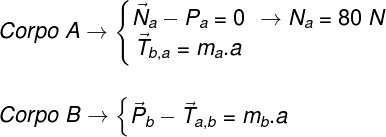
6 – Os corpos movem-se juntos
Como os corpos estão ligados por um fio, a aceleração é igual para os dois, por isso, usamos somente a para os dois corpos.
7 – Resolvendo o sistema de equações
Lembre-se dos pares de ação e reação: Ta,b e Tb,a cancelam-se quando somamos as equações, portanto, ficamos com:
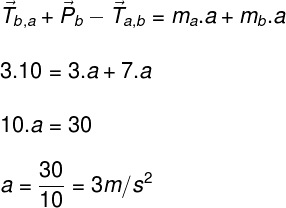
Por fim, para encontrarmos a tração no fio, podemos usar qualquer uma das equações que envolvem as trações:
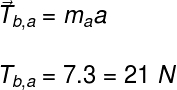
Com isso, encontramos a tração no fio, que equivale a 21 N.
Veja mais em: Exercícios sobre força de tração
Questão 3
3. Dois blocos, A e B, mostrados na figura abaixo e de massas iguais a 2 kg e 3 kg, respectivamente, encostados um no outro, são movidos pela ação de uma força de 15 N sobre o bloco A. Determine a aceleração dos blocos e a intensidade da força que o corpo A faz sobre o corpo B.
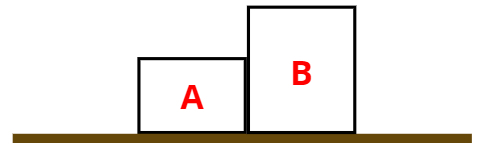
Resolução:
1 – Anotando os dados
Os dados relevantes do exercício são:
ma = 2 kg
mb = 3 kg
|F| = 15 N
2 – Verificando as unidades
Todas as unidades apresentadas estão no Sistema Internacional de Unidades e são compatíveis entre si.
3 – Fazendo o diagrama de forças
Vamos representar todas as forças que agem sobre o sistema de blocos:
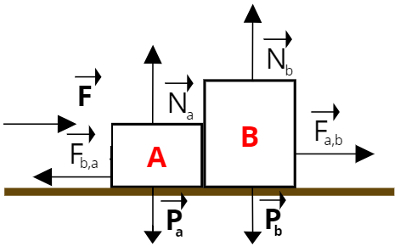
Legenda:
Pa = Peso do bloco A
Pb = Peso do bloco B
Na = Normal do bloco A
Nb = Normal do bloco B
F = Força sobre o sistema de blocos
Fb,a = Força que o bloco B faz no bloco A
F a,b = Força que o bloco A faz no bloco B
4 – Orientando o sistema de coordenadas
Os dois blocos movem-se apenas na direção horizontal, e o sentido do movimento é para a direita. Portanto, todas as forças que apontarem nesse sentido serão tomadas como positivas.
5 – Achando as forças resultantes
As forças resultantes sobre os blocos A e B podem ser escritas de acordo com a orientação do item 5:
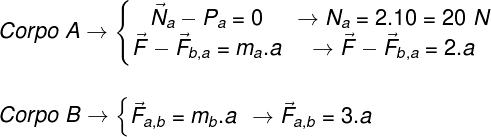
6 – Os corpos movem-se juntos
Os corpos movem-se juntos porque estão pressionados um contra o outro. Dessa forma, a aceleração a é igual para os dois blocos.
7 – Resolvendo o sistema de equações
Para resolver o sistema de equações, devemos lembrar que Fa,b e Fb,a são um par de ação e reação e cancelam-se quando somamos as forças resultantes de A e B, portanto:
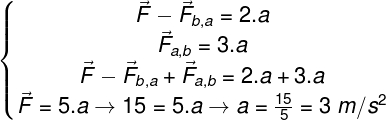
Com a resolução do sistema acima, encontramos que a aceleração deve valer 3 m/s². Usando qualquer uma das forças resultantes encontradas no passo 5, podemos determinar a força que A faz em B ou que B faz em A. Essas forças devem ter valor igual a 9 N.



