Regra de Três Simples e Composta
A regra de três é um processo matemático para a resolução de muitos problemas que envolvem duas ou mais grandezas diretamente ou inversamente proporcionais.
Nesse sentido, na regra de três simples, é necessário que três valores sejam apresentados, para que assim, descubra o quarto valor.
Em outras palavras, a regra de três permite descobrir um valor não identificado, por meio de outros três. A regra de três composta, por sua vez, permite descobrir um valor a partir de três ou mais valores conhecidos.
Grandezas Diretamente Proporcionais
Duas grandezas são diretamente proporcionais quando, o aumento de uma implica no aumento da outra na mesma proporção.
Grandezas Inversamente Proporcionais
Duas grandezas são inversamente proporcionais quando, o aumento de uma implica na redução da outra.
Exercícios Regra de Três Simples
Exercício 1
Para fazer o bolo de aniversário utilizamos 300 gramas de chocolate. No entanto, faremos 5 bolos. Qual a quantidade de chocolate que necessitaremos?
Inicialmente, é importante agrupar as grandezas da mesma espécie em duas colunas, a saber:
| 1 bolo | 300 g |
| 5 bolos | x |
Nesse caso, x é a nossa incógnita, ou seja, o quarto valor a ser descoberto. Feito isso, os valores serão multiplicados de cima para baixo no sentido contrário:
1x = 300 . 5
1x = 1500 g
Logo, para fazer os 5 bolos, precisaremos de 1500 g de chocolate ou 1,5 kg. Note que trata-se de um problema com grandezas diretamente proporcionais, ou seja, fazer mais quatro bolos, ao invés de um, aumentará proporcionalmente a quantidade de chocolate acrescentado nas receitas.
Exercício 2
Para chegar em São Paulo, Lisa demora 3 horas numa velocidade de 80 km/h. Assim, quanto tempo seria necessário para realizar o mesmo percurso numa velocidade de 120 km/h?
Da mesma maneira, agrupa-se os dados correspondentes em duas colunas:
| 80 km/h | 3 horas |
| 120 km/h | x |
Observe que ao aumentar a velocidade, o tempo do percurso diminuirá e, portanto, tratam-se de grandezas inversamente proporcionais. Em outras palavras, o aumento de uma grandeza, implicará na diminuição da outra. Diante disso, invertemos os termos da coluna para realizar a equação:
| 120 km/h | 3 horas |
| 80 km/h | x |
120x = 240
x = 240/120
x = 2 horas
Logo, para fazer o mesmo trajeto aumentando a velocidade o tempo estimado será de 2 horas.
Exercício Regra de Três Composta
Para ler os 8 livros indicados pela professora para realizar o exame final, o estudante precisa estudar 6 horas durante 7 dias para atingir sua meta.
Porém, a data do exame foi antecipada e, portanto, ao invés de 7 dias para estudar, o estudante terá apenas 4 dias. Assim, quantas horas ele terá de estudar por dia, para se preparar para o exame?
Primeiramente, agruparemos numa tabela, os valores fornecidos acima:
| Livros | Horas | Dias |
| 8 | 6 | 7 |
| 8 | x | 4 |
Observe que ao diminuir o número de dias, será necessário aumentar o número de horas de estudo para a leitura dos 8 livros. Portanto, tratam-se de grandezas inversamente proporcionais e, por isso, inverte-se o valor dos dias para realizar a equação:
| Livros | Horas | Dias |
| 8 | 6 | 4 |
| 8 | x | 7 |
6/x = 8/8 . 4/7
6/x = 32/56 = 4/7
6/x = 4/7
4 x = 42
x = 42/4
x = 11 horas
Logo, o estudante precisará estudar 11 horas por dia, durante os 4 dias, a fim de realizar a leitura dos 8 livros indicados pela professora.
Exercícios de Regra de Três
A regra de três é um procedimento usado para a resolução de problemas que envolvem grandezas que são proporcionais.
Pelo fato de ter uma enorme aplicabilidade, é muito importante saber resolver problemas utilizando essa ferramenta.
Portanto, aproveite os exercícios comentados e questões de concursos resolvidas para verificar seus conhecimentos sobre esta matéria.
Exercícios Comentados
Exercício 1
Para alimentar o seu cão, uma pessoa gasta 10 kg de ração a cada 15 dias. Qual a quantidade total de ração consumida por semana, considerando que por dia é sempre colocada a mesma quantidade de ração?
Solução
Devemos sempre começar identificando as grandezas e as suas relações. É muito importante identificar corretamente se as grandezas são diretamente ou inversamente proporcionais.
Neste exercício as grandezas quantidade total de ração consumida e o número de dias são diretamente proporcionais, pois quanto mais dias maior será a quantidade total gasta.
Para melhor visualizar a relação entre as grandezas, podemos usar setas. O sentido da seta aponta para o maior valor de cada grandeza.
As grandezas cujos pares de setas apontam para o mesmo sentido, são diretamente proporcionais e as que apontam em sentidos contrários, são inversamente proporcionais.
Vamos então resolver o exercício proposto, conforme o esquema abaixo:
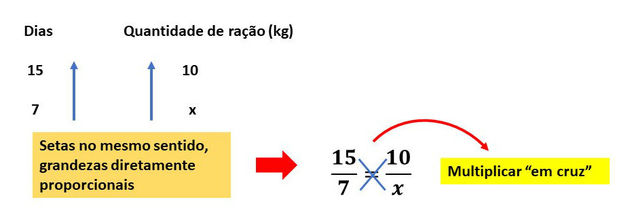
Resolvendo a equação, temos:
Assim, a quantidade de ração consumida por semana é de aproximadamente 4,7 kg.
Exercício 2
Uma torneira enche um tanque em 6 h. Quanto tempo o mesmo tanque levará para encher, se forem utilizadas 4 torneiras com a mesma vazão da torneira anterior?
Solução
Neste problema, as grandezas envolvidas serão número de torneiras e tempo. Contudo, é importante observar que quanto maior o número de torneiras, menor será o tempo para encher o tanque.
Portanto, as grandezas são inversamente proporcionais. Neste caso, ao escrever a proporção, devemos inverter uma das razões, conforme mostramos no esquema abaixo:
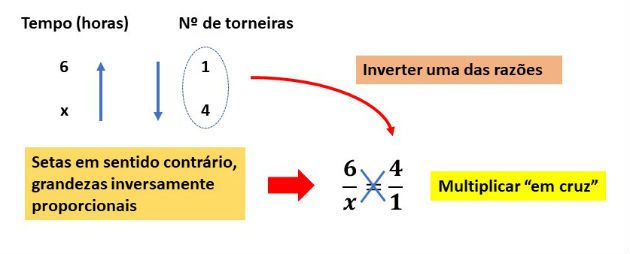
Resolvendo a equação:
Assim, o tanque ficará totalmente cheio em 1,5 h.
Exercício 3
Em uma empresa, 50 funcionários, produzem 200 peças, trabalhando 5 horas por dia. Se o número de funcionários cair pela metade e o número de horas de trabalho por dia passar para 8 horas, quantas peças serão produzidas?
Solução
As grandezas indicadas no problema são: número de funcionários, número de peças e horas trabalhadas por dia. Portanto, temos uma regra de três composta (mais de duas grandezas).
Neste tipo de cálculo, é importante analisar separadamente o que acontece com a incógnita (x), quando mudamos o valor das outras duas grandezas.
Fazendo isso, percebemos que o número de peças será menor se reduzirmos o número de funcionários, portanto, essas grandezas são diretamente proporcionais.
O número de peças aumenta se aumentarmos o número de horas de trabalho por dia. Portanto, também são diretamente proporcionais.
No esquema abaixo, indicamos esse fato através das setas, que apontam para o sentido crescente dos valores.
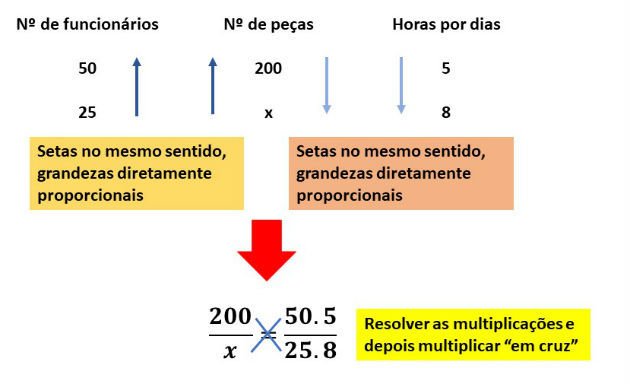
Resolvendo a regra de três, temos:
Assim, serão produzidas 160 peças.
Questões de Concurso Resolvidas
1) Epcar – 2016
Duas máquinas A e B de modelos diferentes, mantendo cada qual sua velocidade de produção constante, produzem juntas n peças iguais, gastando simultaneamente 2 horas e 40 minutos. A máquina A funcionando sozinha, mantendo sua velocidade constante, produziria, em 2 horas de funcionamento, n/2 dessas peças.
É correto afirmar que a máquina B, mantendo sua velocidade de produção constante, produziria também n/2 dessas peças em
a) 40 minutos.
b) 120 minutos.
c) 160 minutos.
d) 240 minutos.


